Practically every photographer knows the phrase “crop factor” (sometimes also called “focal length multiplier” or “focal length magnification”). And many of them are also vaguely aware that it defines a sensor’s size relative to a frame of analog film. But fewer know how exactly it influences the way that photos from phones, compacts, and APS-C DSLR cameras look compared to photos from a full-frame camera. Meanwhile the differences can be quite striking. You’ll see them in the focal length, lens speed, and sharpness.

You’ve probably noticed that you can get significantly different pictures when using the same exposure (aperture, speed, and ISO) on different cameras. Especially as far as depth of field is concerned. This is marvelously visible when you compare examples from opposite ends of the spectrum—large full-frame DSLRs vs. smartphones.

The picture above shows the outputs from a full frame Canon 5D Mark IV DSLR and an LG G4, each with a similar angle of view and similar aperture settings (f/2 for the DSLR and f/1.8 for the phone). The picture from the DSLR, however, has a much blurrier background.

Multiple factors are behind the differences between these devices. But they share one origin—the use of sensors and lenses with different sizes. These sizes, and the properties that result from them, are defined by the crop factor.

Crop Factor Can Tell You Sensor Size

Any hardware manufacturer can make a sensor of any size—and they do. Because its dimensions matter, a camera’s spec sheet will almost always mention either the sensor’s width and height in millimeters (e.g. 36×24 mm) or a diagonal.

Unfortunately for historical reasons this is not the diagonal for the sensor, but rather for the cathode-ray tube (CRT) that would have represented it back in the age of analog video cameras. It’s thus a bit bigger than the sensor. It’s given in fractions of an inch (e.g. 1/4”).

Because it’s hard to compare sensors, and above all the lenses mounted on top of them, when they’re expressed like this, a relative comparison was introduced. And that’s what the crop factor is.

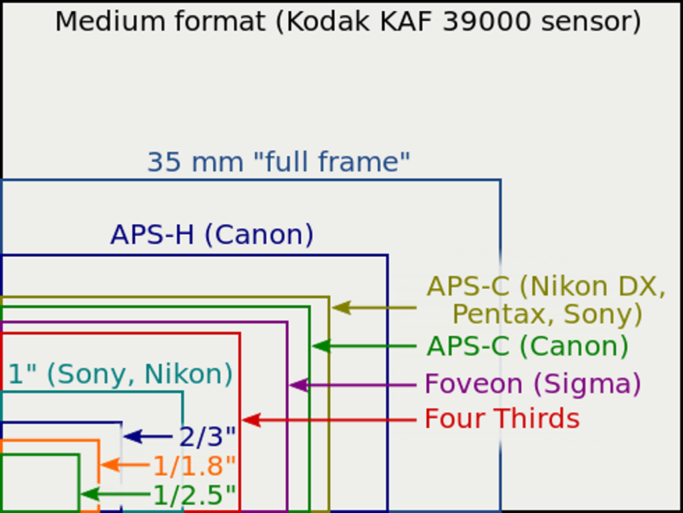
Crop factor expresses how many times smaller (or occasionally larger) a given sensor is than a frame of 35mm film measured as a diagonal. The higher the crop factor, the smaller the sensor.

Smartphones: Sensors Up to 36× Smaller Than in Full Frames

Full frame sensors have a crop factor of 1 and are the reference for crop factors.

Smaller sensors have a crop factor of greater than 1. Typical basic DSLRs have a crop factor of 1.5 or 1.6, mirrorless cameras have a 2, and the sensors in smartphones have around a 6. A smartphone sensor thus has a diagonal 6× smaller than for full-frame DSLRs, and a surface area roughly 36× smaller (“roughly” because they can have different ratios of sides).

Meanwhile in medium-format and larger cameras, the sensors are larger than full-frame and thus have a crop factor of less than 1 (typically from 0.5 to 0.8).

Crop Factor Helps You What’s What in Lenses

The picture below illustrates two different systems with two different sensor sizes, with two lenses that have an identical angle of view. Nevertheless, for lenses what’s presented as their main parameter is focal length. It’s indicated with an f, and it means the distance from the sensor to the lens’s optical center.

Notice how, to get the same angle of view, the lenses need significantly different focal lengths for the different sensor sizes:

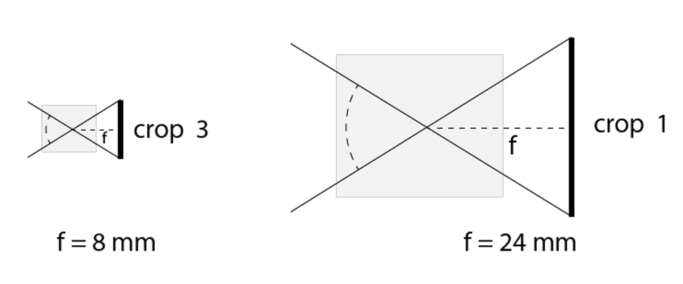
Even though the angle of view can be calculated from the sensor size and the focal length, it’s simpler to just multiply the focal length by the crop factor. This gives you the equivalent focal length. What this tells you is that the given lens has the same angle of view as a specific other lens would have on a full-frame sensor.

For example an 8mm lens on a sensor with a crop factor of 3 is equivalent to a 24mm lens on a full-frame sensor (8mm×3=24 mm).

Crop Factor Influences Lens Speed Too

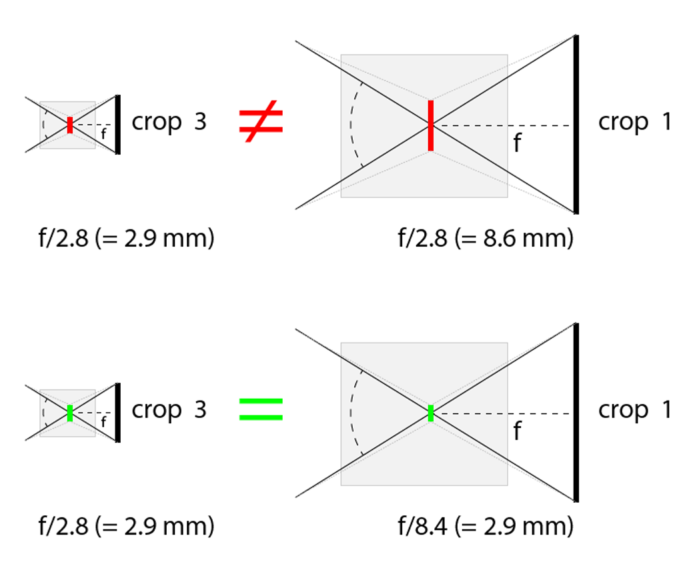
We have a few more things to say here about lenses. Light doesn’t just pass through the one single middle point inside them as was shown in the previous image, and so spec sheets give their aperture value as well, which describes their lens speed. This item is written as f/X, where X is some number, and the item’s true meaning is “focal length divided by X.”

The result is the size of the hole in the middle of the lens that light passes through. For example an aperture value of f/2.8 on a lens with a focal length of 8 mm means an aperture size of 8 mm / 2.8 = 2.9 mm.

If you use the same system as in the previous example with the crop factor of 3, and if your lens is equivalent to a 24mm lens on a full frame, then you need to keep in mind that this conversion only gives you the angle of view. You can’t just say that it corresponds to a 24/2.8 lens, which would have a much larger hole in the middle (8.6 mm); you have to also multiply the aperture value by the crop factor.

So the example 8/2.8 lens is equivalent to a 24/8.4 lens on a full-frame sensor. Pictures from two such sensor-and-lens “sets” will be almost indistinguishable—they’ll just give different noise levels in certain cases.

Don’t let yourself be confused by the statement that a completely different aperture needs to be used on different systems for them to get equivalent behavior. After all, with the higher aperture value, you’ll have to use a much longer exposure or a higher ISO.

This seeming discrepancy is caused by the fact that ISO is also relative to sensor size, and for different sensors, the same number means a different sensitivity and different noise level. To make this overview complete, we should note that you can get photos that are practically visually indistinguishable by using these parameters:

• On the system with crop factor 3: Focal length 8 mm, aperture f/2.8, ISO 100, speed 1/100 s
• On the system with crop factor 1: Focal length 24 mm, aperture f/8.4, ISO 100, speed 1/100 s

The Same Shot on Different Sensors

We took roughly the same shot on four systems with different crop factors. The cameras have different ratios of sides, but otherwise there’s roughly the same angle of view. Note how substantially their focal lengths differ:

In all of these cases, the focal length after multiplication by the crop factor is around 28 or 29 mm.

What Makes Bigger Sensors Better

Even though it’s said that a bigger sensor leads to less noise and can take pictures in deeper darkness, things are more nuanced than that. That’s because these advantages actually come not from the sensor, but from the lens used. If you use a lens with an aperture value of, for example, 2.8 on two different sensors, for each one it amounts to a different lens diameter and thus a different amount of light let through.

For a large sensor it’s then easy to take pictures in deeper darkness, since there’s significantly more light reaching the sensor. But in reality a smaller sensor could also do equally good work if you were to borrow a lens from a larger system and use a “magnifying glass” behind it. And these do exist, in the form of a product called MetaBones SpeedBooster.

So then, is there something in which a large sensor is better? Yes, in its larger dynamic range. This is because it’s less sensitive than a smaller sensor and can expose a shot for a longer time without leading to blowout and completely white skies. So it’s easier for example to  shoot against the sun. Technology marches on, and so even the smaller sensors are gradually being improved, giving them an ever-greater dynamic range. However, this improvement applies for larger sensors as well.

There is essentially a second advantage here. For the larger sensors you can also find large and heavy lenses with fantastic lens speeds. But the above-mentioned MetaBones SpeedBoster can make lenses like these usable on smaller sensors as well, while preserving nearly the same optical properties as the lenses would have when used normally.

What Makes a Large Sensor Better at the Same Lens Speed

Let’s say we want to compare the same angle of view and, alongside it, a specific, numerically identical aperture value (as is written on lenses directly). We’re now comparing lenses with differently sized entry holes, so for all of the sets, the following applies: the smaller the crop factor (i.e. the larger the sensor), the smaller the depth of field and the lower the noise.

Examples from various systems are shown below. Here I did not include the smartphone, because it wasn’t able to “agree with” the other devices on an aperture. For the other cameras, I used an aperture of f/2.8 and a focal length that corresponds to a 28mm angle of view on a full frame.

Here the exposure was f/2.8 / ISO 800 / 1/60 s each time. The illustration shows, from left to right:

• Fujifilm XQ2 with a 6.4mm focal length, with the aperture after multiplying by the crop factor corresponding to f/2.8×3.93=f/11 on a full frame.
• Canon 350D with a focal length of 17 mm, with the aperture corresponding to f/2.8×1.62=f/4.5 on a full frame.
• Canon 5D Mark IV with a focal length of 28 mm, with the aperture being f/2.8 (with a crop factor of 1).

The depth of field is easy to see here; the system with the large sensor (but above all with the large lens) leads in this area.

The Same Focal Length on Different Sensors

To give you the whole picture, I’m also including an example of the effect of crop factor when a numerically identical focal length is used on different sensors. Here it’s a focal length in the 25–26 mm range.

A comparison of the first and last examples looks like this:

If we were to judge strictly from this example, the crop factor would work out to roughly 3.7, but this imprecision come from rounding and from differing ratios of sides.

A Few Examples of Equivalent Lenses

In a lot of systems you’ll find similar lenses, even though they bear completely different numeric designations. But it’s enough to multiply the focal length and the aperture by the crop factor and you’ll get similar lenses. In many cases you can then verify that lenses like these also have similar sizes and weights.

You can always find counterexamples too, such as the Sigma 50/1.4 and the Canon 50/1.4—both made for full-frame cameras, yet completely different in weight (1.79 pounds vs. 0.64).

But otherwise, you can find a lot of lenses that work out to be similar, e.g.

the Panasonic 14-50/2.8-3.5 for Micro Four Thirds (crop factor 2) weighs 1.08 pounds and corresponds to 28-100/5.6–7 for a full frame. You can find similar lenses for a full frame from the trio Sony, Nikon, and Canon, all a bit better in their parameters and thus a bit heavier, such as the Sony FE 24-105/4 with a weight of 1.46 pounds.

Similarly the Sigma 50-100/1.8 for APS-C sensors (crop factor of roughly 1.5) with a weight of 3.31 pounds corresponds to a 75-150/2.7 on a full frame. However, similar lenses of the 70-200/2.8 type have already existed for a long time and here again they’re offered by all of the main full-frame manufacturers. Each of these examples is in the range from 2.87 to 3.31 pounds.

The Lens Is What Counts

While sensor size plays a role, the lens is much more important. And understanding crop factor will help you understand lenses and judge different systems. But lower crop factors and aperture values are not always an advantage.

If for example you’re taking pictures with a high aperture value, while also presenting them at low resolution on the web, it’s nearly irrelevant whether you have a full-frame camera with a heavy lens, or a handy compact that will fit in your pocket.

What’s important is to be able to judge their advantages and disadvantages and evaluate whether a given piece of equipment is a good fit for how you’ll be using it.